Cuprins
- Etape de proiectare:
- 1.Determinarea raspunsului indicial al procesului.
- 2.Determinarea functiei de transfer a partii fixate .
- 3.Reprezentarea grafica a raspunsului indicial al modelului partii fixate.
- 4.Determinarea functiei de transfer a sistemului in bucla inchisa pe baza performantelor specificate.
- 5.Determinarea functiei de transfer a regulatorului prin:
- -alocare de poli;
- -dead-beat extins;
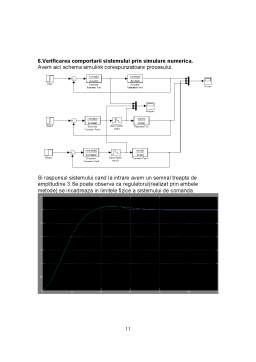
- 6.Verificarea comportarii sistemului prin simulare numerica.
- 7.Verificarea comportarii sistemului in bucla inchisa in timp real(pe instalatie).
Extras din proiect
Sa se proiecteze un regulator numeric astfel incat sistemul in bucla inchisa sa satisfaca urmatoarele performante:
-eroare stationara nula;
-suprareglare mai mica de 5%;
-durata regimului tranzitoriu 60s;
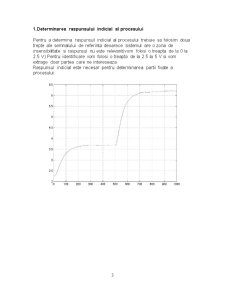
1.Determinarea raspunsului indicial al procesului
Pentru a determina raspunsul indicial al procesului trebuie sa folosim doua trepte ale semnalului de referinta deoarece sistemul are o zona de insensibilitate si raspunsul nu este relevant(vom folosi o treapta de la 0 la 2.5 V).Pentru identificare vom folosi o treapta de la 2.5 la 5 V si vom extrage doar partea care ne intereseaza.
Raspunsul indicial este necesar pentru determinarea partii fixate a procesului.
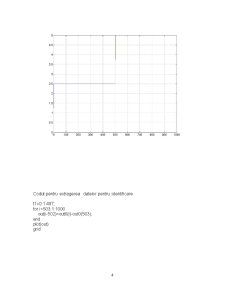
Codul pentru extragerea datelor pentru identificare
t1=0:1:497;
for i=503:1:1000
out(i-502)=out0(i)-out0(503);
end
plot(out)
grid
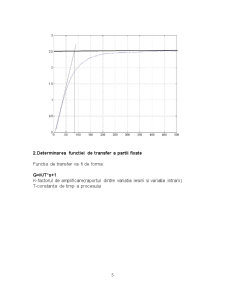
Determinarea functiei de transfer a partii fixate
Functia de transfer va fi de forma:
G=K/T*s+1
K-factorul de amplificare(raportul dintre variatia iesirii si variatia intrarii)
T-constanta de timp a procesului
3.Reprezentarea grafica a raspunsului indicial al modelului partii fixate.
t=0:1:499;
num=[k];
den=[T 1];
gf=tf(num, den); % functia de transfer a partii fixate
gf_out_sim=lsim(gf,2.5*ones(1,length(t)),t);
figure
plot(t,gf_out_sim,'-r');
4.Determinarea functiei de transfer a sistemului in bucla inchisa pe baza performantelor specificate.
Functia de transfer in bucla inchisa este de forma:
G(s)=k/T^2*s^2+2*T*ξ+1=k*ωn^2/s^2+2*ωn*s* ξ+ ωn^2
Codul Matlab pentru calculul acestei functii:
T_impus = 60;
ts = 5.
Preview document
Conținut arhivă zip
- Sisteme Automate cu Esantionare - Reglarea Temperaturii.doc