Determinarea regresiei simple și regresiei multiple - activitățile telefonice din județe în anul 2008

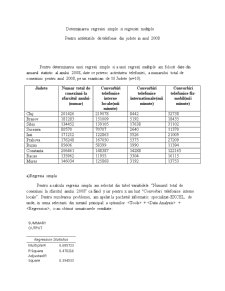
Pentru determinarea unei regresii simple si a unei regresii multiple am folosit date din anuarul statistic al anului 2008, date ce privesc activitatea telefoniei, a numarului total de conexiuni pentru anul 2008, pe un esantioan de 10 Judete (n=10).

Judete Numar total de conexiuni-la sfarsitul anului-

(numar) Convorbiri telefonice interne locale(mii minute) Convorbiri telefonice internationale(mii minute) Convorbiri telefonice fix-mobil(mii minute)

Cluj 201426 219078 8442 32738

Brasov 181283 151009 5192 18435

Sibiu 134452 139105 17638 31102

Suceava 80570 70707 2640 11370

Iasi 171212 122863 5526 21009

Prahova 176248 167050 5375 27209

Buzau 85606 58399 1990 11394

Constanta 206461 148387 14288 122165

Bacau 135962 11955 3304 16115

Mures 146034 125868 3192 13753

a)Regresia simpla

Pentru a calcula regresia simpla am selectat din tabel variabilele “Numarul total de conexiuni la sfarsitul anului 2008” ca fiind y iar pentru x am luat “Convorbiri telefonice interne locale”. Pentru rezolvarea problemei, am apelat la pachetul informatic specializat-EXCEL, de unde, in urma selectarii din meniul principal a optiunilor <Tools> + <Data Analysis> + <Regression>, s-au obtinut urmatoarele rezultate:

SUMMARY OUTPUT

Regression Statistics

Multiple R 0.685723

R Square 0.470216

Adjusted R Square 0.394533

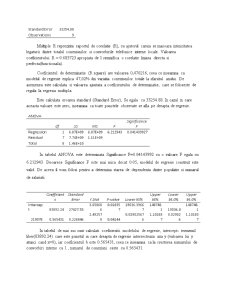
Standard Error 33254.88

Observations 9

Multiple R reprezinta raportul de corelatie (R), cu ajutorul caruia se masoara intensitatea legaturii dintre totalul conexiunilor si convorbirile telefonice interne locale. Valoarea coeficientului R = 0.685723 apropiata de 1 semnifica o corelatie liniara directa si perfecta(functionala).

Coeficientul de determinatie (R square) are valoarea 0,470216, ceea ce inseamna ca modelul de regresie explica 47,02% din variatia conexiunilor totale la sfarsitul anului. De asemenea este calculata si valoarea ajustata a coeficientului de determinatie, care se foloseste de regula la regresia multipla.

Este calculata eroarea standard (Standard Error), Se egala cu 33254.88. In cazul in care aceasta valoare este zero, inseamna ca toate punctele observate se afla pe dreapta de regresie.

ANOVA

df SS MS F Significance F

Regression 1 6.87E+09 6.87E+09 6.212943 0.041439927

Residual 7 7.74E+09 1.11E+09

Total 8 1.46E+10

In tabelul ANOVA este determinata Significance F=0.04143992 cu o valoare F egala cu 6.212943. Deoarece Significance F este mai mica decat 0.05, modelul de regresie construit este valid. De aceea il vom folosi pentru a determina starea de dependenta dintre populatie si numarul de salariati.

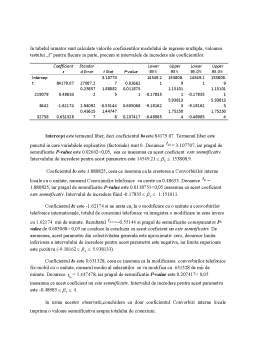
Coefficients Standard Error t Stat P-value Lower 95% Upper 95% Lower 95.0% Upper 95.0%

Intercept 83892.24 27427.55 3.058686 0.018357 19036.39667 148748.1 19036.4 148748.1

219078 0.565431 0.226846 2.492578 0.04144 0.029025676 1.101837 0.029026 1.101837

In tabelul de mai sus sunt calculati coeficientii modelului de regresie, intercept- termenul liber(83892.24) care este punctul in care dreapta de regresie intersecteaza axa y (valoarea lui y atunci cand x=0), iar coeficientul b este 0.565431, ceea ce inseamna ca la cresterea numarului de convorbiri interne cu 1 , numarul de conexiuni ceste cu 0.565431.

Tot aici se testeaza si semnificatia acestor coeficienti, cu ajutorul testului „t”, Deoarece = 3.058686, iar pragul de semnificatie P-value este 0.018357<0,05 inseamna ca acest coeficient este semnificativ. De altfel faptul ca limita inferioara a intervalului de incredere (19036.4 148748.1) pentru acest parametru este negativa, iar limita superioara este pozitiva arata ca parametrul din colectivitatea generala este aproximativ zero. Deoarece = 2.492578, iar pragul de semnificatie P-value este 0.04144< 0,05 inseamna ca acest coeficient este semnificativ. Intervalul de incredere pentru acest parametru este 0.029026 1.101837.

Ecuatia de regresie este: y=83892.24+0.565431x. Modelul se foloseste la realizarea de predictii, dar inainte de aceasta se testeaza validitatea modelului cu ajutorul testului „F”.

In tabelul urmator sunt calculate valorile reziduale (residuals) si valorile previzionate (predicted nr. Total de conexiuni) pe baza modelului de regresie.

RESIDUAL OUTPUT

Observation Predicted 201426 Residuals Standard Residuals

1 169277.4 12005.58 0.385944

2 162546.5 -28094.5 -0.90316

3 123872.2 -43302.2 -1.39204

4 153362.8 17849.2 0.573799

5 178347.5 -2099.5 -0.06749

6 116912.8 -31306.8 -1.00642

7 167794.9 38666.14 1.243001

8 90651.96 45310.04 1.456582

9 155061.9 -9027.92 -0.29022

Datele se succed de-a lungul unei drepte, ceea ce defineste legatura directa dintre cele doua variabile.

b) Regresia multipla

Pentru a calcula regresia multipla am luat y=”Numarul total de conexiuni la sfarsitul anului 2008”,iar pentru x trei valori,si anume: x1=”Convorbiri telefonice interne locale” x2=”Convorbiri telefonice international”, x3=”Convorbiri telefonice fix-mobil”, in excel s-au obtinut urmatoarele tabele: