Calculul de Dimensionare al Unui Motor cu Ardere Internă

Extras din proiect Cum descarc?

TEMA DE PROIECT
Sã se realizeze calculul de dimensionare al unui motor cu ardere internã având
urmatoarele specificatii tehnice:
- Tipul motorului : M.A.C.
- Puterea motorului : Pe = 33 [kW]
- Turatia la puterea maximã : np=4700 [rot/min];
- numãrul de cilindri: i=4 in linie;
3
I. CALCULUL CINEMATIC SI DINAMIC AL MECANISMULUI
BIELÃ-MANIVELÃ
1. CINEMATICA MECANISMULUI BIELÃ-MANIVELÃ
Deplasarea pistonului se poate calcula cu ajutorul relatiei:
( ) (1 cos 2 )
4
cos 1 ..
.
..
. S = r × - a + L × - a [m] (1.1)
Unde: S – cursa pistonului
r – distanta de la axa de rotatie a arborelui la axa fusului maneton, numitã raza
manivelei.
2
S
r = [m] (1.2)
2
0,071 r =
r = 0,035 [m]
. – unghiul de rotatie al arborelui cotit
b – unghiul de rotatie al arborelui cotit
ß – unghiul dintre bielã si axa cilindrului
Se alege
3,2
1 L = (1.3)
Din relatia (1.3) rezultã:
L
= r
b [m] (1.4)
3,2
1
0,035 b =
b = 0,131 [m]
Se alege
3,2
1 L = .
4
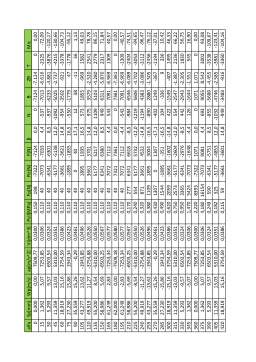
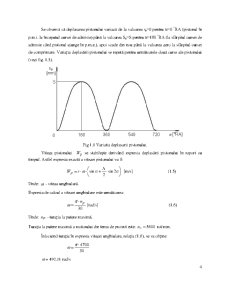
Se observã cã deplasarea pistonului variazã de la valoarea sp=0 pentru a=0 °RA (pistonul în
p.m.i. la începutul cursei de admisie) pânã la valoarea Sp=S pentru a=180 °RA (la sfârsitul cursei de
admisie când pistonul ajunge în p.m.e.), apoi scade din nou pânã la valoarea zero la sfârsitul cursei
de comprimare. Variatia deplasãrii pistonului se repetã pentru urmãtoarele douã curse ale pistonului
(vezi fig. 1.3).
Fig 1.1 Variatia deplasarii pistonului.
Viteza pistonului Wp se stabileste derivând expresia deplasãrii pistonului în raport cu
timpul. Astfel expresia exactã a vitezei pistonului va fi:
sin 2
2
sin .
.
.
..
. Wp = r ×w × a + L × a [m/s] (1.5)
Unde: w - viteza unghiularã.
Expresia de calcul a vitezei unghiulare este urmãtoarea:
30
× n p
=
p
w [rad/s] (1.6)
Unde: nP - turatia la putere maximã.
Turatia la putere maximã a motorului din tema de proiect este: = 5600 P n rot/min.
Înlocuind turatia în expresia vitezei unghiulare, relatia (1.6), se va obtine:
30
w = p × 4700
w = 492,18 rad/s
5
Acceleratia pistonului J p se determinã prin derivarea expresiei vitezei pistonului în raport
cu timpul. Astfel derivând expresia (1.5) se obtine expresia exactã a acceleratiei:
J p = r ×w 2 × (cosa + L× cos 2a ) [m/ s2 ] (1.7)
Deoarece biela executã o miscare complexã de translatie si de rotatie, se considerã cã o parte
din masa bielei este concentratã în punctul de articulatie cu boltul (mBp) si executã o miscare
alternativã de translatie solidar cu grupul piston, iar restul (mBm) este concentratã în punctul de
articulatie cu fusul maneton si executã o miscare de rotatie cu viteza unghiularã . a arborelui cotit
(fig. 1.2).
Fig 1.2 Organizarea maselor in corpul bielei
mB=mBp+mBm [kg] (1.8)
mB=0,17+0,55=0,62 [kg]
Unde: mB [g] – masa totalã a bielei
4
~ D2
m mB B
= ×p × (1.9)
[kg]
D
mB 0,62
4
14,6
2
= ×p × =
S-a constatat experimental cã:
mBp=0,275.mB=0,275·0,62=0,17 [Kg] (1.10)
mBm=0,725.mB=0,725·0,62=0,55 [Kg]
ap [m/s2] – acceleratia pistonului
Forta de inertie a maselor în miscare de rotatie este:
FR=-mR
.r..2 = -10-3 ×1,3× 35,5 × 492,182 = -1179,5 [N] (1.11)
Unde: mR [kg] – masa componentelor aflate în miscare de rotatie
r [m] – raza manivelei;
. [rad/s] – viteza unghiularã a arborelui cotit;
mR=mBm+mcot =0,55+0,75=1,3 [kg].

Fisiere în arhivă (3):

 Calculul de Dimensionare al Unui Motor cu Ardere Interna
 Calculul de Dimensionare al Unui Motor cu Ardere Interna.pdf
 tabel 1.pdf
 tabel 2.pdf

Imagini din acest proiect Cum descarc?