Extras din proiect
Teoriile de micro-macro conectare si relatiile reciproce dintre structura si agenti au devenit o problema centrala a sociologiei (Alexandru et al. 1987). Jocurile intre indivizi si cele la nivel de grup ale analizei sociale sunt semnificative pentru cercetarea in multe subdomenii ale sociologiei, inclusiv in alegerea rationala (Schelling, 1978 ; Coleman 1986 ; Friedman si Hechter 1988), psihologie sociala (Lawler, Ridgeway si Markovsky 1993) si modelarea bazata pe agent (Marcy si Willer 2002). Subiectul de modelare micro-macro a proceselor sociale depinde de urmatoarele doua afirmatii: 1) structura sociala care modeleaza comportamentul individual si atitudini si 2) indivizi care creaza si manipuleaza structuri sociale (Collins 1981). In timp ce prima afirmatie pretinde ca este fundamentala in istoria sociologiei, a doua ramane comparativ mai putin teoretizata si cercetata (Coleman 1990)
In ultimii zece ani teoreticienii de retele, utilizand retelele sociale si reprezentarea de structura, au inceput sa cerceteze problema referitoare la cum indivizii creaza si altereaza retelele sociale (de exemplu Doreian si Stokman, 1997 ; Bala si Goyal, 2000). Analiza de retea s-a concentrat in mod traditional pe configurari statice si modul in care caracteristicile unei concentratii sociale poate influenta alegeri individuale, preferinte si interactiuni sociale. Cercetarea dinamicii retelei este in primul rand preocupata de cum indivizii altereaza structura unei retele. Astfel, cercetarea dinamicii unei retele reprezinta un nou domeniu in studierea relatiei dintre structura sociala si actiunea individuala.
Cercetarea asupra dinamicii retelei in economie si sociologie descrie modul in care structura de relatii dintre actorii sociali evolueaza si se schimba de-a lungul timpului. O mare parte din scrierile de dinamica de retea s-au concentrat pe identificarea de retele care sunt si eficiente (de exemplu satisfactia globala a actorilor comparata cu alternativele) si stabila ( probabil sa persiste) (exemplu Jackson si Wolinsky, 1996 ; Dutta si Mutswami, 1997 ; Bala si Goyal, 2000 ; Dutta si Jackson, 2002). Construirea pe modelele existente ale evolutiei retelei pentru pentru evaluarea probabilitatii retelei, rata aparitiei unei structuri de retea diferita si analizarea echilibrului selectiei, problema care dintre echilibre este mai probabil de obtinut. In particular, examinam rolul critic jucat de « meta-retele », un factor structural care influenteaza cursul dinamicii de retea si probabilitatea retelei observate.
Metaretelele sunt retele de retele, constructii teoretice care portretizeaza diferite retele ca noduri cu conexiuni care exista intre retele care difera una de cealalta prin manipularea unei singure legaturi. Evolutia retelelor este echivalenta cu miscarea in jurul unei metaretele. Pentru ca actorii schimba structura unei retele in care ei coexista se muta intr-o alta locatie in metaretea. Consider ca unele regiuni ale metaretelei sunt mai atractive actorilor decat celelalte. Echilibrul si non-echilibrul retelelor care se gaseste in aceste regiuni sunt mai probabili, pentru ca e posibil ca actorii sa le gaseasca in cursul evolutiei retelei. Astfel, probabilitatea unei retele nu este doar o functie a unei dorinte trasmise dar si a proximitatii ei in metaretea pentru alte retele dorite. Modelele ce urmeaza pun accentul pe un joc de formare de miscare secventiala, utilizand presupuneri din modele anteriore de aceast tip. Actorii isi fac numarul adaugand si stergand legaturi una cate una, intr-o ordine determinata aleator. Mai bine decat presupunerea unor abilitati de calcul estensive, in evaluarea care legaturi trebuie adaugate si care trebuie sterse, actorii considera efectele imediate ale adaugarii sau stergerii. Aceste modele permit deasemenea specificatii ale probabilitatilor de retele de echilibru si de non-echilibru.
In sectiunile care urmeaza, va fi detaliat conceptul de metaretea, vor fi revizuite cercetari relevante asupra dinamicii retelei, in termeni de modelare si vor fi prezentate supozitii de modelare. In Modelul 1, in care actorii incadrati retelei incearca sa maximizeze “gaurile de structura” (Burt, 1992) prin manipularea strategica a retelei, cel mai accesibil echilibru de retea in metaretea este si cel mai probabil. In Modelul 2, in care actorii manipuleaza reteaua lor pentru a maximize validitatea informatiei, acest rezultat este replicat chiar si atunci cand cel mai probabil echilibru de retea este Pareto-eficient. In al treilea rand pentru ambele modele vom arata ca in drumul catre echilibru evolutia retelei este foarte probabil sa treaca prin relele non echilibrate care stau in vecinatati mai accesibile metaretelei. Vom concluziona discutand rezultatele si propunand directiile viitoare in modelarea evolutiei retelei.
METARETELE
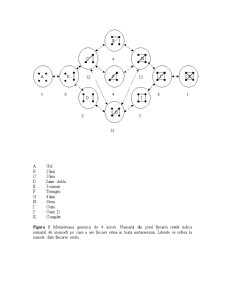
Dupa cum am mentionat mai devreme, metaretelele sunt retele de posibile retele in cadrul carora retelele care difera intre ele printr-o singura veriga de manipulare sunt legate. Evolutia retelei poate fi astfel conceptualizata ca o miscare in jurul unei metaretele. De Exemplu figura 1 indica o metaretea de 4 actori. Metareteaua de 4 actori include toate posibilele retele de 4 actori ca si noduri. Conexiunile dintre noduri reprezinta “retele de vecinatate”, retele care sunt la o distanta de o veriga manipulatoare. Astfel, ca si grup de patru actori, manipuland legaturile de retea conectandu-le, ele traseasa o cale prin metareteaua Figurii 1.
Este un subiect de discutie daca geografia metaretelei afecteaza obiceiul schimbarii structurale determinand accesibilitatea diferitelor retele. Aceste efecte se intampla pentru ca desirabilitatea vecinatatilor de retea contureaza accesibilitatea retelelor din vecinatate. Retelele mai dorite sunt mai accesibile pentru ca ele sunt mai probabile sa atraga actori in timp ce iau decizii pentru a altera reteaua in care coexista. Rezultatul este ca dinamica retelei este posibil sa se bazeze pe echilibrul intern sau in apropierea vecinatatilor unei metaretele atractive. Desirabilitatea unei vecinatati de retea de echilibru poate avea un efect mai mare asupra unui selectii de echilibru decat asupra desirabilitatii relative ale a echilibrului in sine, asa cum am demonstrat in Modelul 2.
Preview document
Conținut arhivă zip
- Modele Matematice Aplicate in Sociologie.doc