Partea I: analiza dispersionala ANOVA Potrivit Institutului National de Statistica, in Romania, in perioada 1990-2006 s-a recoltat un volum de 139668,7 mc de lemn. http://www.insse.ro/ cms/rw/pages/statRegionale.ro.do Grupam setul de date dupa tipul de lemn recoltat si aplicam ANOVA pentru a vedea daca exista diferente semnificative intre volumul de lemn recoltat in medie din cele 5 categorii. Ipotezele: H0: u1 = u2 = u3 = u4 = u5 ; H1: cel putin doua medii sunt diferite. Volum de lemn recoltat in Romania 1990-2006 Rasinoase Fag Stejar Diverse specii tari Diverse specii moi 5813,4 4957,8 2045,4 2070,7 1761,7 4973,1 4214,7 1550,5 1774,4 1300 5346,1 4508,4 1333 1731 1366,2 4915,3 4260,1 1287,8 1673,3 1273,8 7165,6 4439,2 1494,8 1805,2 1478,3 7139 4747,7 1531,6 1823 1450,2 6356,6 5412 1694,4 2030,5 1588,6 6060,5 4794,2 1586,1 1852,1 1378,4 5765 4997,2 1632,2 1914,6 1375 Folosind Excel se obtin rezultatele: Anova: Single Factor SUMMARY Groups Count Sum Average Variance Rasinoase 9 53535 5948,2889 688928,66 Fag 9 42331 4703,4778 150816,01 Stejar 9 14156 1572,8667 48606,287 Diverse specii tari 9 16675 1852,7556 17404,158 Diverse specii moi 9 12972 1441,3556 23476,96 In tabelul SUMARY sunt trecute date despre cele 5 populatii: - Numarul de unitati din fiecare populatie: 9; - Volumul total de lemn recoltat in perioada 1990-2006 pentru fiecare populatie; - Volumul mediu de lemn recoltat in fiecare an pentru fiecare populatie; - Dispersia populatiilor. ANOVA Source of Variation SS df MS F P-value F crit Between Groups 155904090 4 38976022 209,72168 3E-26 2,606 Within Groups 7433856,59 40 185846,41 Total 163337946 44 In tabelul ANOVA este calculata statistica F: Putem afirma cu o probabilitate de 95 % ca tipul de lemn are o influenta semnificativa asupra volumului de lemn recoltat, deoarece statistica calculata F=209,72168 este mult mai mare decat Fcritic=2,606. Mai mult decat atat, P-value=3*10-26 ne garanteaza rezultatele pana la o probabilitate de (1 - 3 * 10 - 26 ) * 100. Asadar se respinge ipoteza nula conform careia mediile populatiilor sunt egale si se accepta ipoteza alternativa conform careia cel putin doua medii sunt semnificativ diferite. Partea II: modele econometrice de regresie unifactoriala Pentru un set de 17 valori, reprezentand numarul de cinematografe din Romania din anii 1990-2006 si numarul de spectatori din aceeasi perioada (http://www.insse.ro/cms/files/pdf/ro/cap9.pdf), se va testa daca exista o legatura liniara simpla intre cele doua variabile. 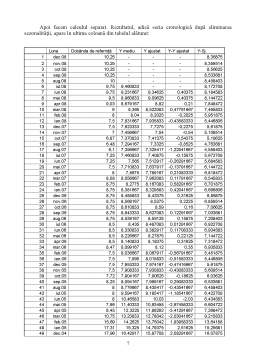Datele de intrare sunt: Ani Cinematografe Spectatori (mii) 1990 4637 130144 1991 3222 67444 1992 1771 46086 1993 1470 33720 1994 713 25915 1995 626 17007 1996 484 12639 1997 468 9422 1998 313 6834 1999 321 4196 2000 279 4450 2001 264 5728 2002 230 5317 2003 191 4527 2004 151 4002 2005 85 2830 2006 73 2777 Consideram X, variabila independenta numarul de cinematografe si Y, variabila dependenta numarul de spectatori. Propunem urmatorul model: Y= a + b*X caruia ii vom testa validitatea folosind Reggression din Excel. Obtinem urmatorul rezultat: SUMMARY OUTPUT Regression Statistics Multiple R 0,986836265 R Square 0,973845813 Adjusted R Square 0,972102201 Standard Error 5527,569203 Observations 17
Plateste in siguranta cu cardul bancar si beneficiezi de garantia 200% din partea Proiecte.ro.
